
プログラミングを学ぶ人「Decision Tree、決定木って何だろう?」
こんな方に向けた記事です。
Pythonで機械学習の勉強を始めると初めましての言葉にたくさん遭遇します。
決定木、ランダムフォレスト、勾配ブースティング木・・・。
木とか森とか、機械学習と何の関係があるんだろう。
私は出会う度にこのような感情を抱いていました。Pythonのデータ分析では木とか森とかこの類の言葉がやたらと出てくるんです。
新しい言葉に出会った時拒否反応が出る気持ち、本当によくわかります。
ただ決定木、ランダムフォレスト、そして勾配ブースティング木などの木関連の予測モデルはこの決定木さえ理解してしまえばすぐに理解できます。
私もこれらの予測モデルの理論を理解するのに非常に時間がかかりました。私は理解が早い方ではないのでみなさんはもっと早く理解できると思います。
なので今回は実際に医療の現場のデータ分析ではこのように用いられているという具体例を紹介していきます。
一緒に勉強していきましょう。
本記事の想定読者
- プログラミング初心者でとりあえず触れてみたい人
- 機械学習で何ができるか知りたい人
- Pythonの勉強を始めて間もない人
機械学習の決定木(Decision Tree)

まず結論から。決定木(Decision Tree)は樹形図によってデータを分類しながら分析していく手法です。
決定木という言葉自体はアルゴリズム、つまり計算方法や計算手法を指すのではありません。
以下の紹介する、図のような患者の特徴による分岐のみを表す概念です。ここが混同しやすいので注意が必要です。
決定木を用いたアルゴリズムはC4.5やCART(Classification and Regression Tree)などが該当します。
具体例を見ていきましょう。
今回「心不全患者30人の予後(死亡or生存)」を追跡したstudyを想定してみましょう。
従来の研究を参考に生死のリスクとなり得る様々な因子が抽出され予後を追跡されているとします。
今回は試しに“喫煙歴”、“BMI”、“飲酒歴”を構成要素とした決定木を想定してみましょう。
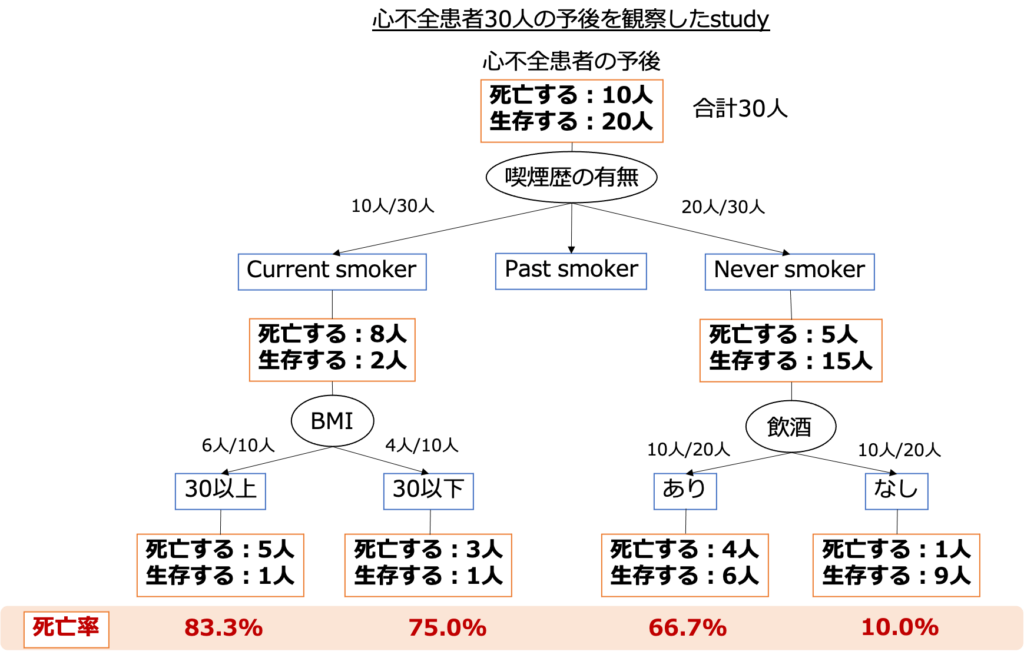
これが決定木です。今回の結果ではCurrent smokerかつBMI30以上の患者で死亡率が最も高いことがわかりました。
この決定木を応用した予後予測アルゴリズムがランダムフォレストや勾配ブースティング木なんです。
ランダムフォレストや勾配ブースティング木はこの決定木をどのように組み合わせるかであるので、最小単位は決定木から構成されています。
このデータを特徴ごとに分類していく概念こそが決定木です。
ポイント
- 決定木はデータを特徴ごとに樹形図状に分類していく概念である。
- 決定木を用いたアルゴリズムはC4.5やCART(Classification and Regression Tree)などが存在する。
- 決定木の応用アルゴリズムにはランダムフォレストや勾配ブースティング木などがある。
決定木を用いたアルゴリズム

決定木を用いたアルゴリズムは以下のような手順で進んでいきます。
決定木の仕組み
- データを分割するのに最適なAttribute Selection Measures(ASM)(属性選択尺度)を選択する。
- 選択した特性によってデータをより小さな集団に分割していく。
- ①全てのタプルが同じ特性に分類される。 ②特性分類が残ることなく使用される。 ③全症例がどこかのグループへ分類される。 この3つのどれかを達成するまで決定木を様々な組み合わせで構築し続ける
簡単に言うと、集められたデータを最も良く分類する特徴の組み合わせを見つけ出すまで決定木構築をひたすらするんです。
具体的いうと、今回集められたデータには、結果的にある特徴の組み合わせを持ったAというグループ、別の特徴の組み合わせを持ったBというグループ、さらに別の特徴の組み合わせを持ったCというグループがあったとします。これを元のデータからしっかりと分類できる組み合わせの特徴を見つけ出し、正しく分類するということです。
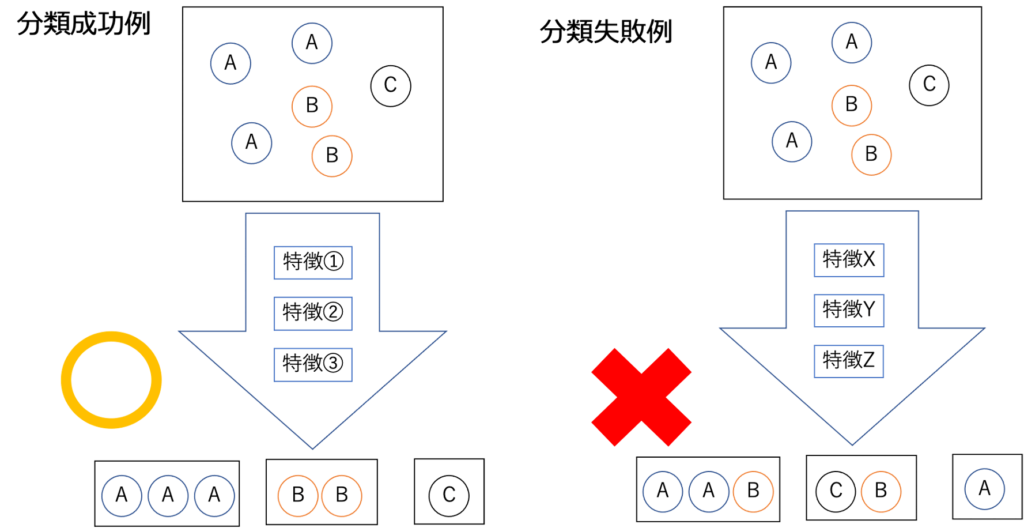
このようにデータを正しく分類できるまで無数のパターンを試していくのが決定木を用いたアルゴリズムです。
この特徴の正しい組み合わせを導き出す時にエントロピー、ジニ係数という概念が登場します。
ひとつずつゆっくりと勉強していきましょう。
エントロピー
エントロピーとは熱力学および統計力学において定義される示量性の状態量である。統計力学において系の微視的な「煩雑さ」を表す物理量。
<引用>https://ja.wikipedia.org/wiki/エントロピー
Wikipediaにエントロピーはこのように説明されています。エントロピーは物事の煩雑さを表す指標なんですね。
エントロピーは物事の煩雑さを表す指標で整っている場合エントロピーは低くなり、乱れている場合にエントロピーは高くなります。
これから数式でエントロピーの理解を深めていきます。正直、エントロピーの概念を理解することができていれば数式に関しては理解する必要はありません。数式が苦手な人は読み飛ばしてください。
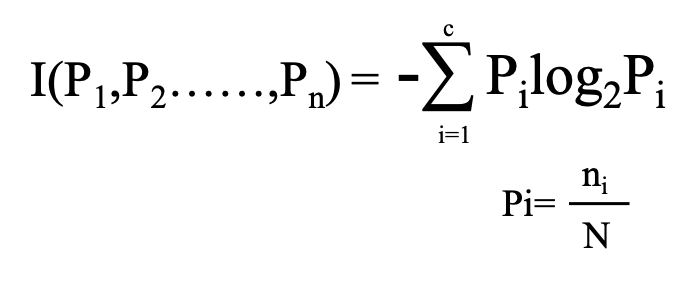
C:目的変数のクラスの数 N:データサンプル総数 ni:クラスiに属するデータ数
エントロピーはこのような式で表すことができます。
この式で最もデータが整然としている状態、そして最もデータが煩雑な状態を想定してみましょう。
最も整然とした状態は全てのデータが同じ分類なること。このような式になります。
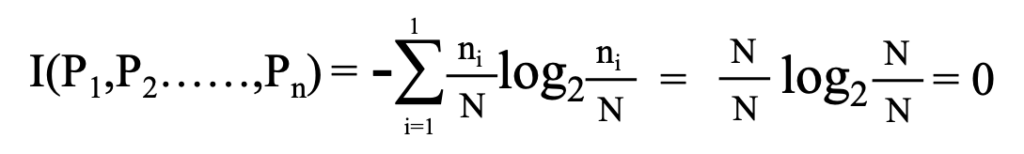
整然とした状態ではエントロピーが小さくなることがわかります。
次に最も煩雑とした状態を想定してみましょう。最も煩雑とした状態はデータ一つ一つ全てが異なるクラスに分類されている状態です。
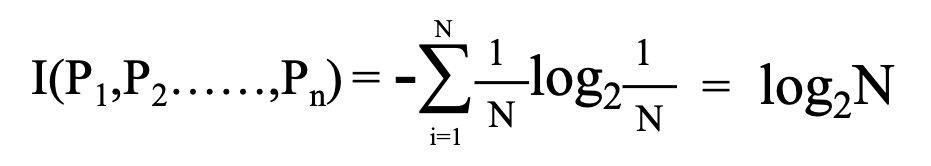
煩雑とした状態ではエントロピーが大きくなることがわかります。
<対数変換の復習>
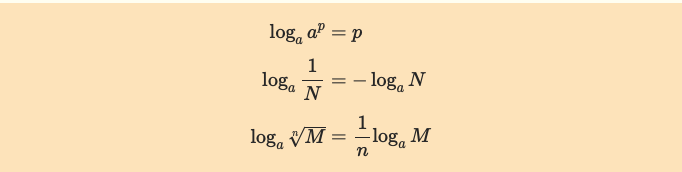
つまり、より良くデータを分類するためにはよりエントロピーが小さくなるような特徴の組み合わせを模索する必要があります。
それではある特徴でデータを分類した時、うまく分類できたかどうかをどのように判断すれば良いでしょうか。
これはエントロピーからGainというものを算出することで判断することができます。
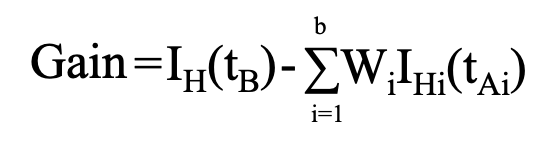
b:分岐の数 tB:分岐前のノード tA:分岐後のノード Wi:重み(分岐前に対するデータの量の割合)
これはつまりこのような式で表すことができます。
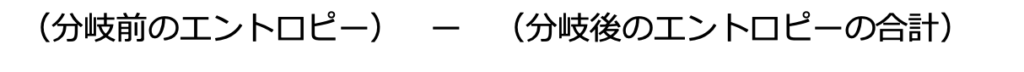
正しく分類できていれば分岐前は煩雑で分岐後は整然としているはずです。つまりこの式の値は大きくなるはずです。
この Gainを最大化するのが決定木を用いたアルゴリズムの一つ、C4.5です。
ジニ係数
ジニ係数とは主に社会における所得の不平等さを測る指標である。
<引用>https://ja.wikipedia.org/wiki/ジニ係数
Wikipediaに紹介されているようにジニ係数は社会の所得格差を表す指標として使用されています。
Gini係数は以下の式で表されます。
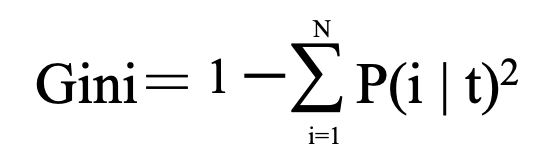
N:データサンプル総数
再度、最もデータが整然としている場合を想定してみます。
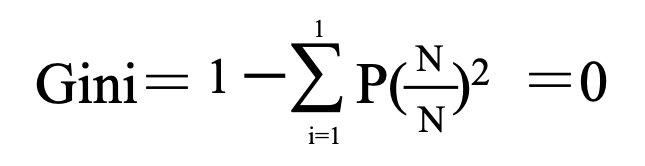
つまりデータが整然とすればするほどGiniは0に近づいていきます。
Gini係数もエントロピーと同様に分類が正しくできているかどうか、このような式でGainを表す事ができます
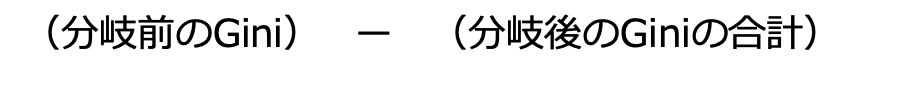
このGiniによるGainを最大化するのが決定木を用いたアルゴリズムの一つであるCARTです。
ポイント
- 決定木を用いたアルゴリズムにはC4.5やCARTがある。
- エントロピーの差を最大化させるのがC4.5である。
- Giniの差を最大化させるのがCARTである。
【参考にさせていただきました】
<Qiita>
<対数logの復習>
<ジニ係数について>
さいごに

みなさんいかがでしたでしょうか。
今回はデータ分析の基本的な考え方となる決定木について一緒に勉強しました。数式などが出てきて後半内容が少し難しくなりました。今回の内容を復習していきましょう。
まず最初に。エントロピーやGini係数、そしてその算出式などは概念をより深く理解するためのものです。これらは正直、しっかりと理解できていなくてもデータ解析自体は問題なく行うことが出来ます。
なので数式に苦手意識がある人はまず決定木という考え方を理解さえしてしまえば細かい数式などは全く理解せずに次に進んでしまいましょう!ここでプログラミングに苦手意識を覚える必要は全くありません!
決定木は樹形図状にデータを分類しながら分析していく手法でした。
決定木を用いたアルゴリズムにはC4.5やCARTなどがあります。中でもエントロピーを指標にしたものがC4.5、Giniを指標にしたものがCARTと呼ばれます。
それぞれ概念自体の理解はとっつきにくいと思います。
具体例で実際にイメージしながらじっくりと理解していくのが良いと思います。
機械学習はプログラミング言語のPythonを用いれば、今持っている自分のパソコンですぐに実践することができます。
英語論文になっている手法もしっかりと勉強すれば、自分のパソコンで出来ます。
このサイトでは、プログラミングに興味のある医学生、医師のための情報を発信しております。
プログラミングの学習方法には大きく分けて、「独学」と「プログラミングスクール」の2つがあります。
当サイトでは一貫してプログラミングスクールを利用することをおすすめしています。
なぜなら、独学で勉強した私が非常に苦労したからです。
また私はプログラミングを学習するにあたり、師匠・メンターのような存在がいました。
わからないところは教えてもらっていました。
そのような環境でなければ0から独学で勉強するのはとても効率が悪いと思います。
詳しくは、プログラミングの独学は難しいです【私の失敗談】で紹介しています。
この記事が一人でも多くのプログラミングに興味のある方のお役に立てば幸いです。




