
プログラミングを学ぶ人「ニューラルネットワークの損失関数ってどんなもの?」
こんな方に向けた記事です。
今回はニューラルネットワークの損失関数について一緒に勉強していきましょう。
損失関数とは一言で表すとニューラルネットワークの性能の悪さを表す指標です。
損失関数は予測と実際の値のズレの大きさを表す関数であり、この損失関数を小さくする、つまり予測の実際の値が可能な限り小さくなるようにニューラルネットワークのパラメータを調整します。
今回は損失関数の概要、そしてニューラルネットワークで用いられる代表的な損失関数について見て参りましょう。
本記事の学習目標
- 損失関数の概要を理解する。
- 代表的な2つの損失関数について理解する。
ニューラルネットワークの損失関数について解説

損失関数とはニューラルネットワークによる予測値が実際の値からどのくらい離れているかを表した関数のことです。
この損失関数が可能な限り小さくなるようにニューラルネットワークにおいてパラメータをチューニングしていくことになります。
できるだけ小さな損失関数の場所を探すためにパラメータの微分(勾配)を計算し、その値を手掛かりにパラメータの値を更新していきます。
ある損失関数に対しての微分の値がマイナス、つまり下向きの傾きを持っていたとすると、パラメータを正の方向へ変化させることで損失関数を小さくすることができます。
またある損失関数の微分の値がプラス、つまり上向きの傾きを持っていたとすると、パラメータを負の方向へ変化させることで損失関数を小さくすることができます。
このように次々と損失関数の微分値を基にパラメータを更新していきます。微分の値が0になるとパラメータを正負のどちらに動かしても損失関数が変化しないため、パラメータの更新はストップすることになります。
パラメータの更新に、「性能の悪さ」を指標にすることに違和感を感じるかもしれません。しかし、性能の悪さにマイナスを掛けるとそれは「どれだけ性能が良いか」という指標として解釈することができます。
性能の悪さを指標にすることと性能の良さを指標にすることは本質的には同じであると言えます。
では、なぜ認識制度そのものを指標にしないのか。
それは認識制度の差はごく小さく、微分がほとんどの場所で0になってしまい、パラメータの更新ができなくなってしまうからです。
認識制度そのものはパラメータの微小な変化にはほとんど反応を示さず、反応があったとしても不連続に変化してしまします。これはニューラルネットワークの活性化関数にステップ関数を使うとうまく学習ができないことと同じです。
ニューラルネットワークや活性化関数についてはこちらの記事で解説しているので是非目を通してみてください。
一方で損失関数はパラメータの少しの変化によって連続的に変化するためパラメータの調整を効果的に行うことができます。
代表的な損失関数
損失関数として用いられる関数はいくつか存在します。
今回はその中でも代表的な2つの関数、2乗和誤差、交差エントロピー誤差をご紹介します。
ポイント
- 2乗和誤差
- 交差エントロピー誤差
2乗和誤差

損失関数のうち最もポピュラーなものがこの2乗和誤差です。2乗和誤差は上の式で表されます。
ykはニューラルネットワークの出力、tkは実際の値(教師データ)を表します。予測値と実際の値の差を2乗したものの合計を2で割ったものが2乗和誤差になります。
この2乗和誤差は小さい方がより良い値ということになります。つまり、この2乗和誤差が小さくなるようにニューラルネットワークのパラメータを調整します。
例えば、ある動物の写真を犬か、猫か、ウサギかを予測するニューラルネットワークを想定します。
y=[0.15, 0.6, 0.25]
t=[0, 1, 0]
yはニューラルネットワークの出力を表します。左から犬、猫、ウサギの順です。この出力はソフトマックス関数の出力であり、それぞれの値を確立として近似することができます。
つまり今回は写真が犬である確率は0.15, つまり15%、猫である確率は0.6, つまり60%、ウサギである確率は0.25, 25%ということになります。
実際の値tを見てみると写真は1である猫が正解ということになります。ちなみにこの正解、不正解を1, 0で表す手法をone-hot encodingと呼びます。
このニューラルネットワークによる予測の2乗和誤差を計算してみましょう。
import numpy as np y=[0.15, 0.6, 0.25] t=[0, 1, 0] def mean_squared_error(y,t): return 0.5 * np.sum((y-t)**2) mean_squared_error(np.array(y), np.array(t)) #0.12250000000000001
実際のコードで2乗和誤差を実装しました。今回は正解である猫の確立が最も高くなっています。それではニューラルネットワークによる予測が正解である猫ではなく犬である確率が最も高かった場合を考えてみましょう。
import numpy as np y=[0.55, 0.25, 0.2] t=[0, 1, 0] def mean_squared_error(y,t): return 0.5 * np.sum((y-t)**2) mean_squared_error(np.array(y), np.array(t)) #0.4525
すると二乗和誤差は0.4525とより高い値になります。つまり実際の値と予測の値の乖離が大きく、より不正確な予測になっていることが表されています。
一つ目の例の方がニューラルネットワークによる予測結果が実際のデータにより結合していることが表されています。
交差エントロピー誤差

ykはニューラルネットワークの出力、tkは実際の値(教師データ)を表します。tkはone-hot encodingで正解を1、それ以外を0と表すものとします。
つまりこの交差エントロピー誤差は正解ラベルが1に対応する出力の自然対数を計算するだけになります。つまり先述の1つ目の例を考えてみます。
ある動物の写真を犬か、猫か、ウサギかを予測するニューラルネットワークを想定します。
y=[0.15, 0.6, 0.25]
t=[0, 1, 0]
この場合交差エントロピー誤差は-log0.6=0.51となります。
二つ目の例で考えてみます。
y=[0.55, 0.25, 0.2]
t=[0, 1, 0]
この場合の交差エントロピー誤差は-log0.25=1.38となります。
ここで自然対数のグラフをmatplotlibを用いて作成してみましょう。
import numpy as np import matplotlib.pyplot as plt x=np.arange(0,1,0.01) #0から1まで0.01刻みで配列を作る y=np.log(x) plt.plot(x,y) plt.show()
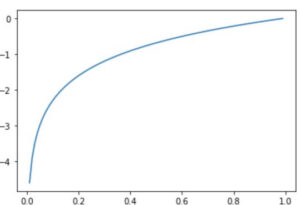
y=logxの式はx=1の時y=0になることがわかります。つまり、予測値が1に近ければ近いほどyは0に近づくことがわかります。
つまり交差エントロピー誤差は0に近い程より良い値ということになります。
それでは先述の例で交差エントロピー誤差を実装してみましょう。
import numpy as np y=[0.15, 0.6, 0.25] t=[0, 1, 0] def cross_entropy_error(y,t): delta=1e-7 return -np.sum(t*np.log(y+delta)) cross_entropy_error(np.array(y),np.array(t)) #0.510825457099338
y=[0.55, 0.25, 0.2]
t=[0, 1, 0]
この時は先ほどの計算の様に交差エントロピー誤差は0.51となります。
交差エントロピー誤差の実装ではyに1e-7を足して計算しています。この1e-7は1 x 10-7を表します。
np.log0はマイナス無限大になってしまいます。マイナス無限大になってしまうとそれ以上の計算をすることができなくなります。これを防ぐために予め微小な数である1e-7を足しています。
同様に先述の二つ目の例も実装してみます。
import numpy as np y=[0.55, 0.25, 0.2] t=[0, 1, 0] def cross_entropy_error(y,t): delta=1e-7 return -np.sum(t*np.log(y+delta)) cross_entropy_error(np.array(y),np.array(t)) #1.3862939611199705
y=[0.55, 0.25, 0.2]
t=[0, 1, 0]
この時は先ほどの計算の様に交差エントロピー誤差は1.38となります。
つまりニューラルネットワークによる予測の値が実際の値に近い程0に近い数字になることがわかります。
さいごに

いかがでしょうか。今回はニューラルネットワークの損失関数ついて一緒に勉強しました。
ニューラルネットワークのパラメータ選択で一般に用いられる代表的な手法になります。この記事が少しでも皆様の役に立てば幸いです。
機械学習はプログラミング言語のPythonを用いれば、今持っている自分のパソコンですぐに実践することができます。
英語論文になっている手法もしっかりと勉強すれば、自分のパソコンで出来ます。
このサイトでは、プログラミングに興味のある医学生、医師のための情報を発信しております。
プログラミングの学習方法には大きく分けて、「独学」と「プログラミングスクール」の2つがあります。
当サイトでは一貫してプログラミングスクールを利用することをおすすめしています。
なぜなら、独学で勉強した私が非常に苦労したからです。
また私はプログラミングを学習するにあたり、師匠・メンターのような存在がいました。
わからないところは教えてもらっていました。
そのような環境でなければ0から独学で勉強するのはとても効率が悪いと思います。
詳しくは、プログラミングの独学は難しいです【私の失敗談】で紹介しています。
この記事が一人でも多くのプログラミングに興味のある方のお役に立てば幸いです。




