
プログラミングを学ぶ人「パーセプトロンって何だろう?」
こんな方に向けた記事です。
今回はPython機械学習のパーセプトロンについて一緒に勉強していきましょう。
パーセプトロンは後々出てくるニューラルネットワークというPythonの代表的なモデルの基本となる考え方です。
ニューラルネットワークについては、ニューラルネットワークの損失関数について解説【コードあり】で詳しく紹介しています。
ニューラルネットワークは元々はディープラーニングで使われる手法です。ディープラーニングでは10層以上あるようなニューラルネットワークが用いられます。しかし、テーブルデータに対しては中間層が2〜4層程度のニューラルネットワークが用いられます。
ニューラルネットワークを理解するにはニューラルネットワークの構成要素となるパーセプトロンについて理解する必要があります。今回はこのパーセプトロンについて一緒に勉強していきましょう。
ニューラルネットワークも医学論文でたびたび用いられている手法の一つであり、Python機械学習の基本的なモデルの一つです。
それでは一緒に勉強していきましょう。
本記事の学習目標
- パーセプトロンとは何か理解する。
- パーセプトロンの実践を理解する。
- パーセプトロンの限界を理解する。
パーセプトロン
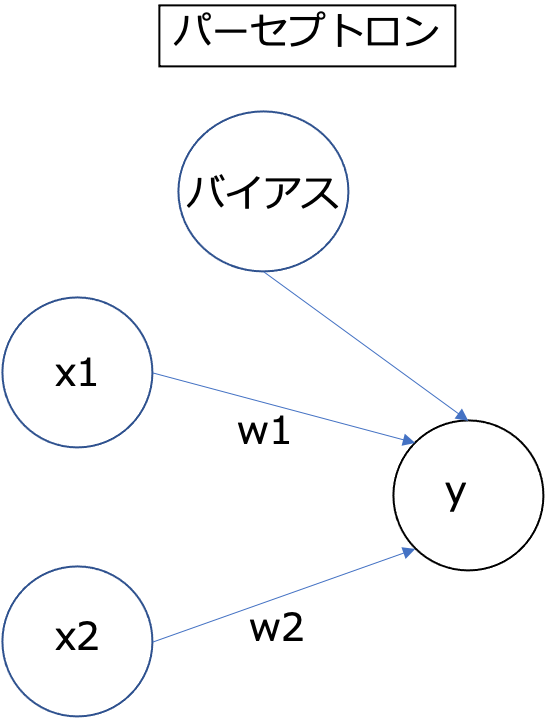
パーセプトロンは人間の神経伝達回路を真似て作られた概念であると考えられています。
パーセプトロンは複数の信号を入力として受け取り、ひとつの信号を出力します。
x1、x2は入力信号、w1、w2は重みを表します。○はそれぞれノードやニューロンと呼ばれます。
入力信号はニューロンに送られる際にそれぞれ固有の重みが掛け算されます。
ニューロンでは送られてきた信号の総和がある限界値(閾値:θ)を超えた時に1として出力されます。
重み(w)
重みは出力の重要度を調整する因子です。例えばx1をより重要な入力とする場合は1例としてw1=0.8、w2=0.2のように調整します。
バイアス(b)
バイアスは出力の0もしくは1に関して1を出力する度合いを調整する因子です。バイアスは出力x1、x2のように重さを乗じる必要がなくそのままの値として使用されます。
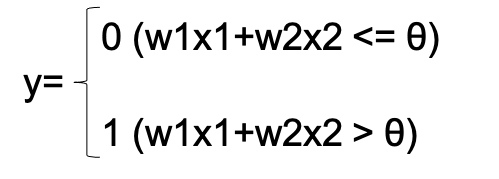
パーセプトロンの動作原理を数式で表すとこのようになります。
例えば、次のような値を考えてみましょう。
(例1 ANDゲート)
θ: 1
x1: 0
x2: 1
w1: 0.6
w2: 0.4
バイアス: -0.3
出力:-0.3 + 0x0.6 + 1x0.4 = 0.1 (<1)
出力:0
(例2 ORゲート)
θ: 0
x1: 1
x2: 0
w1: 0.8
w2: 0.8
バイアス: -0.3
出力:-0.3 + 1x0.8 + 0x0.8 = 0.5 (>0)
出力:1
(例3 NANDゲート)
θ: 0
x1: 1
x2: 1
w1: -0.5
w2: -0.6
バイアス: 0.3
出力:0.3 + 1x(-0.5) + 1x(-0.6)=-0.8
出力:0
これがパーセプトロンの考え方です。
ANDゲート、ORゲート、NADNゲートについては下で解説していきます。
このように重みとバイアスを調整することで出力をコントロールすることが出来ます。これがパーセプトロンの最大の特徴でありディープラーニングの基本的な仕組みになっています。
パーセプトロンの実践
パーセプトロンには代表的な3つの論理回路があります。
パーセプトロンの代表的な3つの論理回路
- ANDゲート
- NANDゲート
- ORゲート
それぞれについて見て参りましょう。
ANDゲート
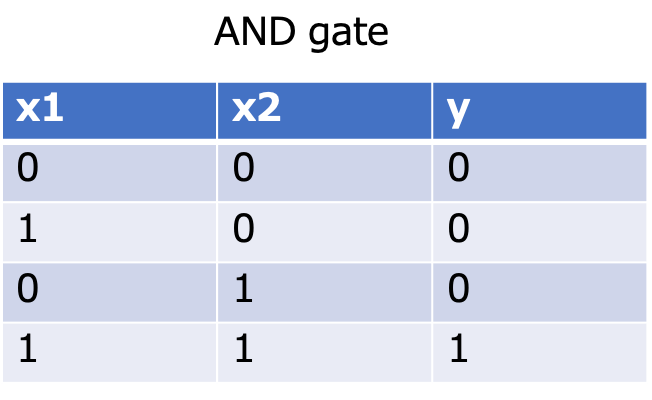
ANDゲートは2つの出力(x1, x2)が共に1の時だけ1を出力し、それ以外では0を出力します。
上で紹介した例1がANDゲートにあたります。
このANDゲートをpythonで実践するとこのようになります。
# パーセプトロンのANDゲート def and_gate(x1, x2): w1 = 0.6 w2 = 0.8 b = -0.3 出力 = b + x1 * w1 + x2 * w2 if 出力 <= 1: y = 0 elif 出力 > 1: y = 1 return y #出力結果 # 確認用コード print(and_gate(0, 0)) #0 print(and_gate(1, 0)) #0 print(and_gate(0, 1)) #0 print(and_gate(1, 1)) #1
print()の使い方はこちらの記事こちらの記事で解説しているので是非一度目を通してみてください。
ORゲート
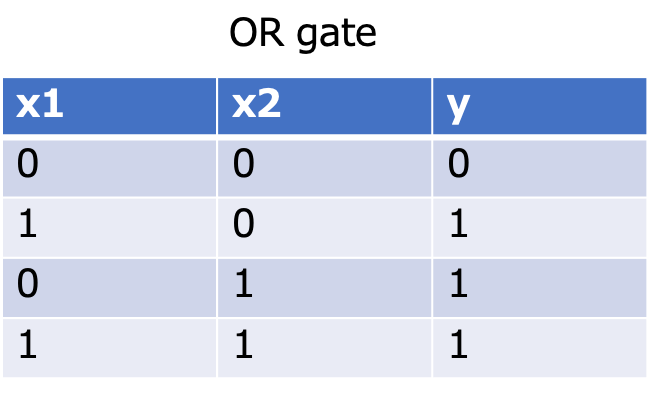
ORゲートは2つの出力(x1, x2)のどちらかが1の時に1を出力し、共に0である時に0を出力します。
上で紹介した例2がORゲートにあたります。
このORゲートをpythonで実践するとこのようになります。
# パーセプトロンのORゲート def and_gate(x1, x2): w1 = 0.8 w2 = 0.8 b = -0.3 出力 = b + x1 * w1 + x2 * w2 if 出力 <= 0: y = 0 elif 出力 > 0: y = 1 return y #出力結果 # 確認用コード print(and_gate(0, 0)) #0 print(and_gate(1, 0)) #1 print(and_gate(0, 1)) #1 print(and_gate(1, 1)) #1
NANDゲート
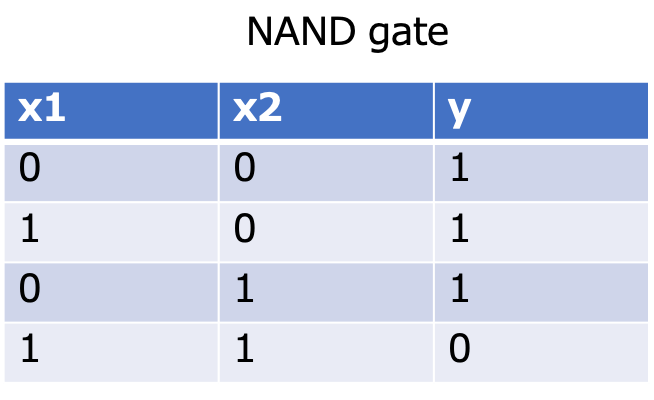
NANDゲートは2つの出力(x1, x2)が共に1の時に0を出力し、それ以外では1を出力します。
ANDゲートの真反対ですね。
このNANDゲートをpythonで実践するとこのようになります。
# パーセプトロンのNANDゲート def and_gate(x1, x2): w1 = -0.5 w2 = -0.6 b = 0.3 出力 = b + x1 * w1 + x2 * w2 if 出力 <= 0: y = 0 elif 出力 > 0: y = 1 return y #出力結果 # 確認用コード print(and_gate(0, 0)) #1 print(and_gate(1, 0)) #0 print(and_gate(0, 1)) #0 print(and_gate(1, 1)) #0
パーセプトロンの限界
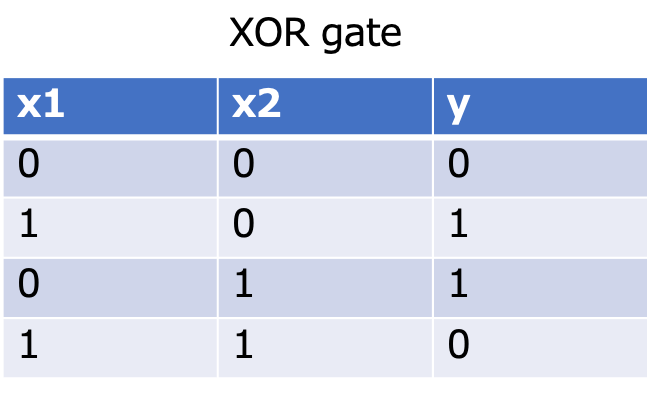
XORゲートとは出力x1、x2どちらかが1の時だけ1を出力します。
パーセプトロンではこのXORゲートを実現することができません。
XORゲートを実現するにはパーセプトロンで層を重ねる必要があります。
このパーセプトロンの層を重ねるという考え方がニューラルネットワークに繋がります。
パーセプトロンの問題点を解決するべく生まれたのがニューラルネットワークです。
さいごに

今回はPython機械学習の基本的な考え方の一つであるパーセプトロンについて一緒に勉強しました。
パーセプトロンとは
パーセプトロンは人間の神経伝達回路を真似て作られた概念であると考えられています。
パーセプトロンは複数の信号を入力として受け取り、ひとつの信号を出力します。
パーセプトロンの実践
- ANDゲート
- NANDゲート
- ORゲート
パーセプトロンの限界
XORゲートを実現することができない。
それぞれ概念自体の理解はとっつきにくいと思います。
具体例で実際にイメージしながらじっくりと理解していくのが良いと思います。
機械学習はプログラミング言語のPythonを用いれば、今持っている自分のパソコンですぐに実践することができます。
英語論文になっている手法もしっかりと勉強すれば、自分のパソコンで出来ます。
このサイトでは、プログラミングに興味のある医学生、医師のための情報を発信しております。
プログラミングの学習方法には大きく分けて、「独学」と「プログラミングスクール」の2つがあります。
当サイトでは一貫してプログラミングスクールを利用することをおすすめしています。
なぜなら、独学で勉強した私が非常に苦労したからです。
また私はプログラミングを学習するにあたり、師匠・メンターのような存在がいました。
わからないところは教えてもらっていました。
そのような環境でなければ0から独学で勉強するのはとても効率が悪いと思います。
詳しくは、プログラミングの独学は難しいです【私の失敗談】で紹介しています。
この記事が一人でも多くのプログラミングに興味のある方のお役に立てば幸いです。




