機械学習の評価指標についてわかりやすく解説

 

プログラミングを学ぶ人「機械学習の評価指標って何があるの？どうなっているの？」

 

 

 

こんな方に向けた記事です。

 

今回はPython機械学習で重要な評価指標について一緒に勉強していきましょう。

 

評価指標とは作成したモデルの性能を測る指標のことです。

 

作成した予測モデルは正しく評価しなければ作成した意味がありません。

 

分析コンペなどでは評価指標に基づきより良いモデルを作ることを競っています。

 

感度が高いモデルが良いのか、特異度が高いモデルが良いのか、何をよりよりモデルとするか一貫した評価指標を設けることが重要です。

 

機械学習には３種類のタスクがあり、タスク毎に評価指標が設けられています。

 

今回はタスクごとの主な評価指標とその性能についてわかりやすく解説していきます。

 

 

機械学習の評価指標

 

 

機械学習の3種類のタスクはこちらです。

 

3種類のタスクについては【機械学習】タスクについてわかりやすく解説（3種類あります）で詳しく紹介しています。

 

3種類のタスクそれぞれに評価指標が設けられています。

 

今回は中でも評価指標が重要な回帰タスク、分類タスクの評価指標について解説していきます。

 

ひとつずつじっくりと見て参りましょう。

 

回帰タスクにおける評価指標

 

 

RMSE(Root Mean Square Error)

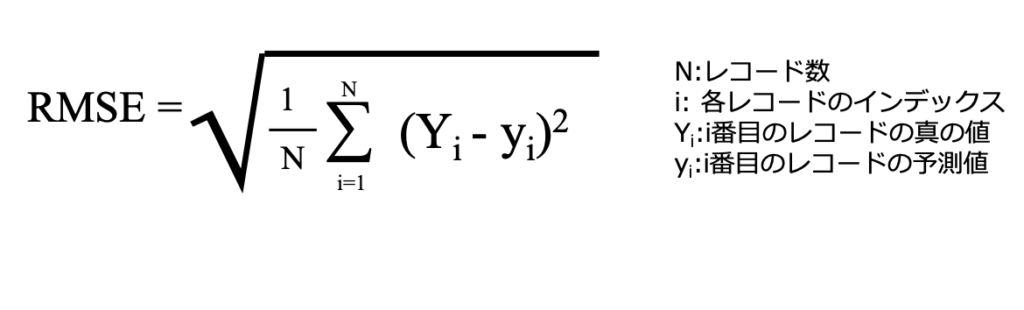
RMSEは回帰タスクにおける最も代表的な評価指標です。

 

それぞれの目的変数の真の値からそれぞれの予測値の差を二乗し、平均した後に平方根にします。

 

実際の値と予測値が近づくほど、RMSE は小さくなります。逆に実際の値と予測値が離れる程、RMSEは大きくなります。

 

よってRMSEは外れ値の影響を受けやすいと言われています。

 

仮に一つの代表値で予測を行う場合、RMSEを最小化する予測値は平均値になります。

 

 

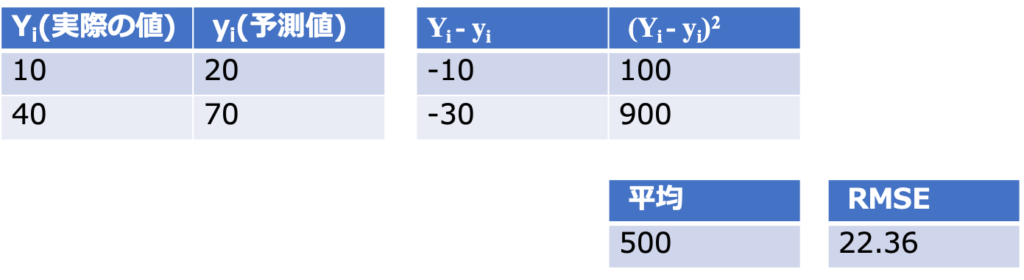
具体的に見るとこのようになります。

 

これをpythonで実践してみましょう。

 

import numpy as np
from sklearn.metrics import mean_squared_error

#Yi: 実際の値　yi：予測値
Yi=[10, 40]
yi=[20, 70]

rmse=np.sqrt(mean_squared_error(Yi, yi))
print(rmse)

#22.360679774997898

 

scikit learnのmetricsモジュールのmean_squared_errorを用いて求めることができます。

 

22.36と手で計算した時と同じ値が得られました。

 

RMSLE(Root Mean Logarithmic Square Error)

 

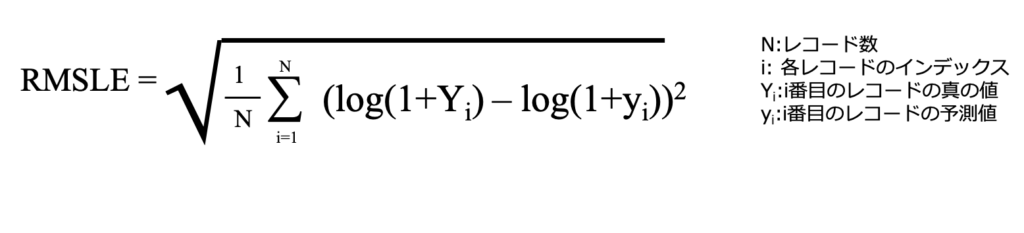
RMSLEは実際の値と予測値の対数をそれぞれとった後の差の２乗の平均を平方根ととって計算される指標です。

 

対数を取るにあたって実際の値が０であった時に負の値になってしまうことを避けるために１を加えてから対数をとります。

 

scikit learnのmetricsモジュールのmean_squared_log_errorを用いて求めることができます。

 

import numpy as np
from sklearn.metrics import mean_squared_log_error

#Yi: 実際の値　yi：予測値
Yi=[100, 0, 400]
yi=[200, 10, 200]

rmse=np.sqrt(mean_squared_log_error(Yi, yi))
print(rmse)

#1.4944905400842203

MAE(mean absolute error)

 

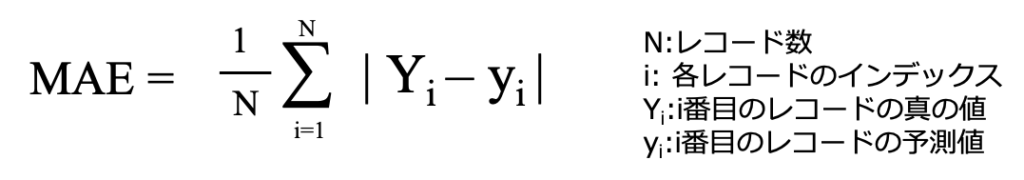
MAEは実際の値と予測値の差の絶対値を平均することで計算される指標です。

 

仮に一つの値でMAEを最小化するには予測値は中央値になります。

 

MAEは二乗をしていないので外れ値の影響を受けにくいと言われています。

 

scikit learnのmetricsモジュールのmean_absolute_errorを用いて求めることができます。

 

import numpy as np
from sklearn.metrics import mean_absolute_error

#Yi: 実際の値　yi：予測値
Yi=[10, 40]
yi=[20, 70]

mae=mean_absolute_error(Yi, yi)
print(mae)

#20.0

R² (決定係数)

 

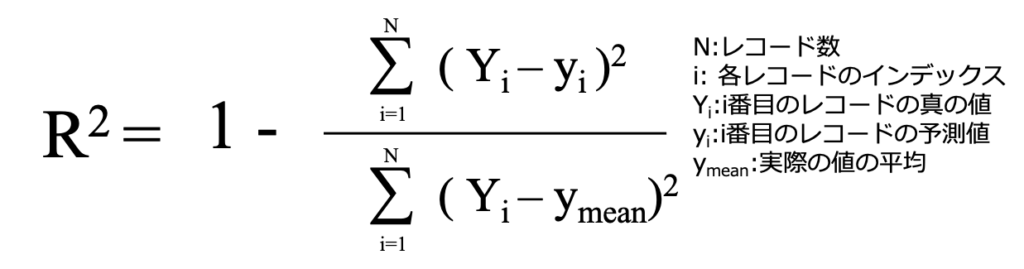
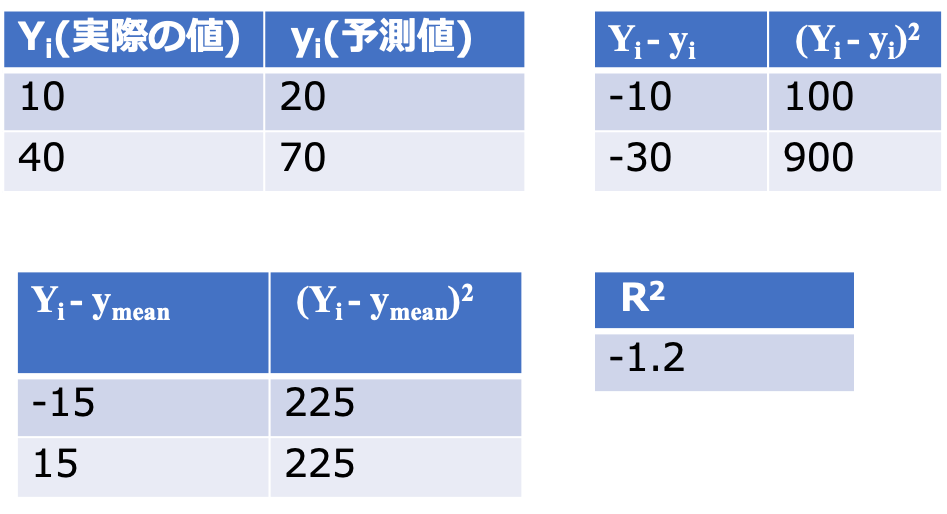
決定係数は最大値が１であり、１に近づく程精度の高い予測ができていることになります。

 

つまり、実際の値と予測値が近い程決定係数が１に近づき、実際の値と予測値が遠くなると決定係数は１から離れた数字になります。

 

scikit learnのmetricsモジュールのr2_scoreを用いて求めることができます。

 

import numpy as np
from sklearn.metrics import r2_score

#Yi: 実際の値　yi：予測値
Yi=[10, 40]
yi=[20, 70]

r2=r2_score(Yi, yi)
print(r2)

#-1.2222222222222223

 

分類タスクにおける評価指標

 

 

分類タスクの代表的な評価指標はこれらのようなものが挙げられます。

 

評価指標それぞれを見ていく前にまずは基本的な考え方である混合行列（Confusion matrix）について勉強しましょう。

 

混合行列（Confusion matrix）

 

第一に混合行列（confusion matrix）自体は評価指標ではありません。

 

混合行列（confusion matrix）とは分類タスクにおいて、予測と実際の分類を行列形式にまとめたものです。

 

分類タスクの根幹となる重要な考え方なので是非理解しておいてください。

 

 

 

scikit learnのmetricsモジュールのconfusion_matrixを用いて求めることができます。

 

import numpy as np
from sklearn.metrics import confusion_matrix

# 0, 1で表される二値分類の実際の値と予測値
y_true = [0, 0, 0, 0, 0, 1, 1, 0, 1]
y_pred = [0, 0, 1, 0, 1, 0, 1, 0, 0]

tp = np.sum((np.array(y_true) == 1) & (np.array(y_pred) == 1))
tn = np.sum((np.array(y_true) == 0) & (np.array(y_pred) == 0))
fp = np.sum((np.array(y_true) == 0) & (np.array(y_pred) == 1))
fn = np.sum((np.array(y_true) == 1) & (np.array(y_pred) == 0))

confusion_matrix1 = np.array([[tp, fp],
                              [fn, tn]])
print(confusion_matrix1)

#[[1 2]
 [2 4]]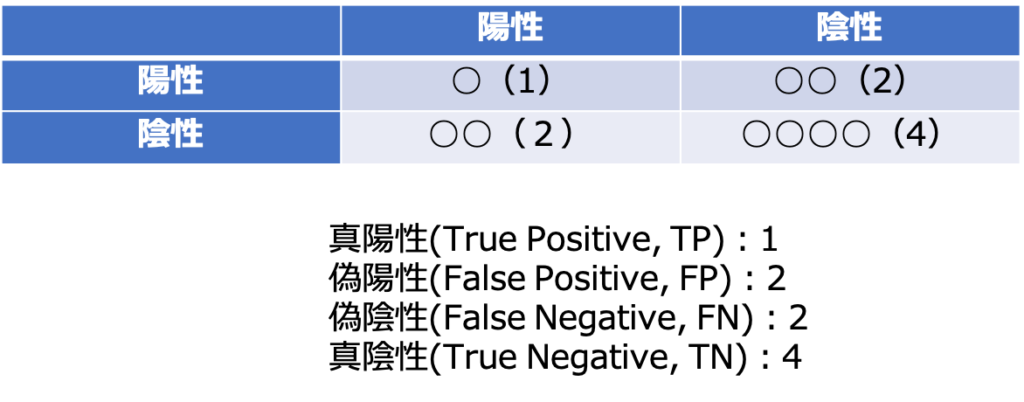

Accuracy（正確性）

 

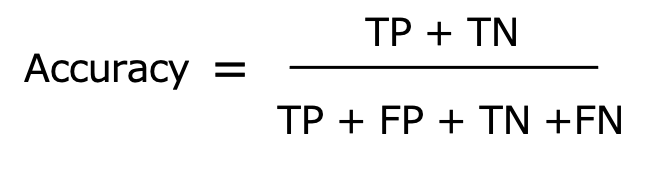
Accuracyは全ての予測のうち、正解した予測の割合を表します。

 

ある予測モデルが10個中７個の予測が正解すれば、Accuracyは0.7となります。

 

注意すべきはAccuracyが高ければ良いモデルであると言うことはできない点です。

 

例えば[1, 1, 1, 1, 1, 1, 1, 1, 1, 0]という実際の値を[1, 1, 1, 1, 1, 1, 1, 1, 1, 1]と予測したとしましょう。これはAccuracy 0.9となり一見良いモデルに思えます。しかし、本来この予測で区別したいはずのたった１つの負例を予測できなかったことになり、本当に良いモデルかどうか疑問が残ります。

 

非常に理解しやすい評価指標ですね。

 

scikit learnのmetricsモジュールのaccuracy_scoreを用いて求めることができます。

 

import numpy as np
from sklearn.metrics import accuracy_score

# 0, 1で表される二値分類の実際の値と予測値
y_true = [0, 0, 0, 0, 0, 1, 1, 0, 1]
y_pred = [0, 0, 1, 0, 1, 0, 1, 0, 0]

accuracy=accuracy_score(y_true, y_pred)

print(accuracy)

#0.5555555555555556

Precision(適合性)

 

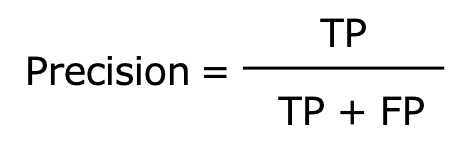
Precisionは陽性と予測したもののうち、実際に陽性であるものの割合を表します。

 

これも直感的に理解しやすい指標ですね。

 

適合率を重視するときはFN(False Negative)が発生することが許容できる場合です。

 

適合率は例えば、ある新薬を投薬した場合に効果が出る可能性のある患者をリストアップする場合などに有効です。

 

scikit learnのmetricsモジュールのprecision_scoreを用いて求めることができます。

 

import numpy as np
from sklearn.metrics import precision_score

# 0, 1で表される二値分類の実際の値と予測値
y_true = [0, 0, 0, 0, 0, 1, 1, 0, 1]
y_pred = [0, 0, 1, 0, 1, 0, 1, 0, 0]

precision=precision_score(y_true, y_pred)

print(precision)

#0.3333333333333333

Recall(再現性)

 

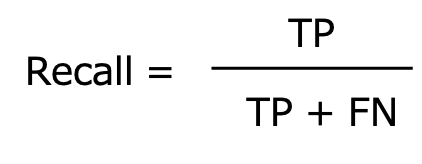
Recallは再現性の他、感度、True Positive Rate、TPRなどと呼ばれます。

 

Recallは実際に陽性であるもののうち、陽性と正しく予測できたものの割合を表します。

 

再現率を重視するときはFP(False Positive)が発生することが許容できる場合です。

 

感度は医療者の方は馴染みが深いですね。

 

再現率の利用シーンは、がん診断のように、取りこぼしを減らしたいときです。

 

scikit learnのmetricsモジュールのrecall_scoreを用いて求めることができます。

 

import numpy as np
from sklearn.metrics import recall_score

# 0, 1で表される二値分類の実際の値と予測値
y_true = [0, 0, 0, 0, 0, 1, 1, 0, 1]
y_pred = [0, 0, 1, 0, 1, 0, 1, 0, 0]

recall=recall_score(y_true, y_pred)

print(recall)

#0.3333333333333333

F1-score

 

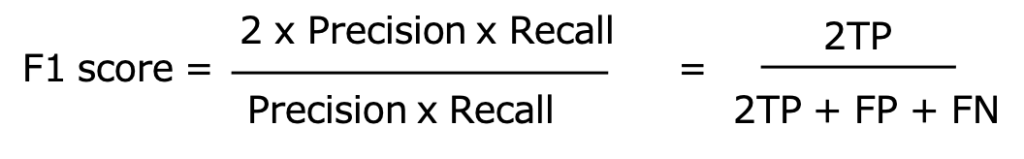
F1-score、Fβscoreは対照的な特徴を持つ適合率と再現率の調和平均です。

 

対照的な２つの指標をうまく盛り込んだ指標であると言えます。

 

分子が適合率と再現率の掛け算になっているため、片方が極端に低い場合に、正しく低い評価をつけることができます。

 

scikit learnのmetricsモジュールのf1_scoreを用いて求めることができます。

 

import numpy as np
from sklearn.metrics import f1_score

# 0, 1で表される二値分類の実際の値と予測値
y_true = [0, 0, 0, 0, 0, 1, 1, 0, 1]
y_pred = [0, 0, 1, 0, 1, 0, 1, 0, 0]

f1=f1_score(y_true, y_pred)

print(f1)

#0.3333333333333333

Log loss

 

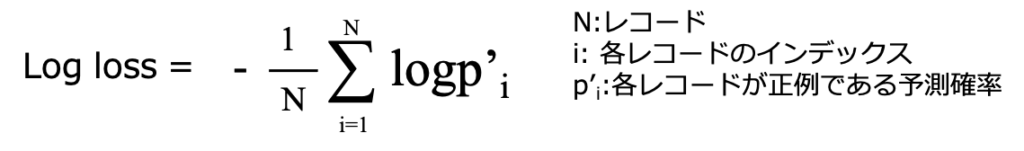
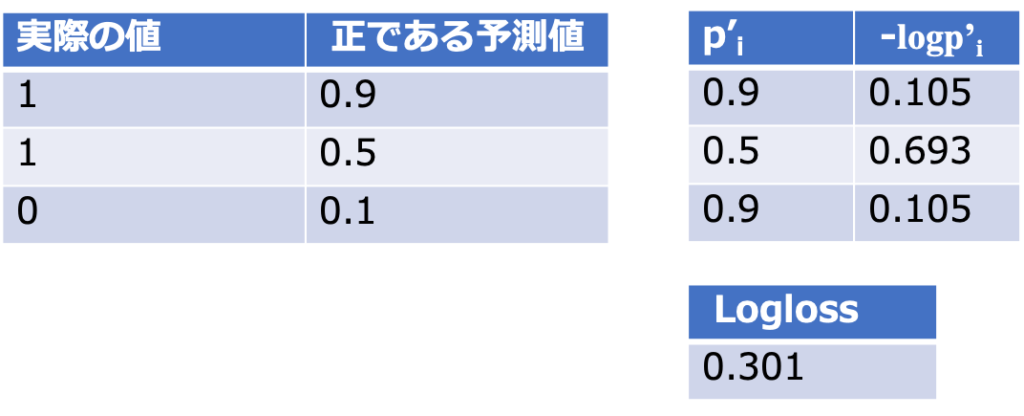
病気である場合に、どれくらいの確率で病気と分類されるか知りたい、こういった場合にLog lossが使用されます。

 

Accuracyではある閾値をカットオフとし閾値以上を1、閾値以下が０として計算されます。

 

Log lossではどのくらいの確率で陽性であるかを数値のまま出力します。

 

 

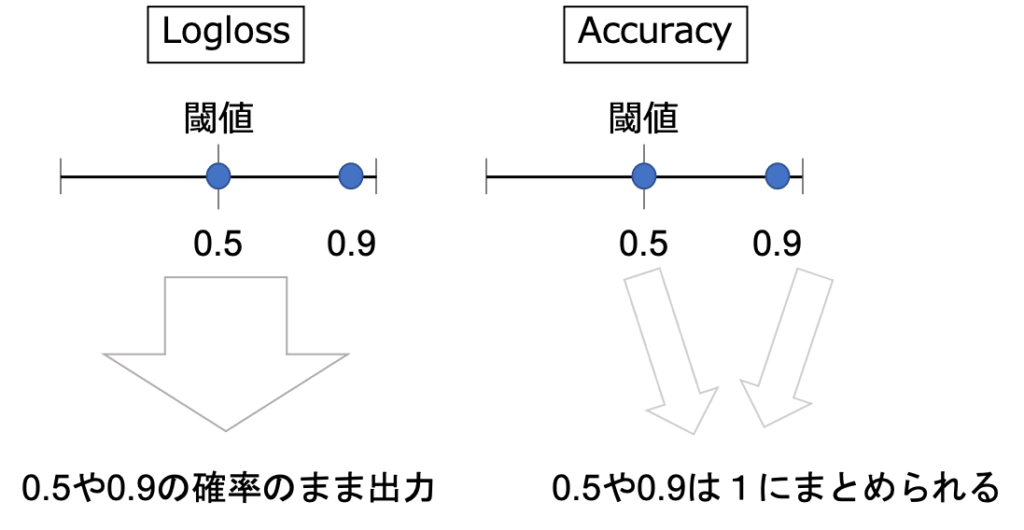
真の値を予測している確率とLoglossスコアの相関図はこのようになります。

 

 

 

図の通り、確率を正しく予測できている時にLoglossの値は小さくなります。

 

scikit learnのmetricsモジュールのlog_lossを用いて求めることができます。

 

import numpy as np
from sklearn.metrics import log_loss

# 0, 1で表される二値分類の実際の値と正である予測確率
y_true = [0, 0, 0, 0, 0, 1, 1, 0, 1]
y_pred = [0.1, 0.2, 0.1, 0.4, 0.2, 0.7, 0.6, 0.2, 0.9]

log_loss=log_loss(y_true, y_pred)

print(log_loss)

#0.2626487102652024

AUC(Area Under the ROC Curve)

 

馴染みが深い方も多いと思います。

 

こちらも分類タスクの代表的な評価指標の一つです。

 

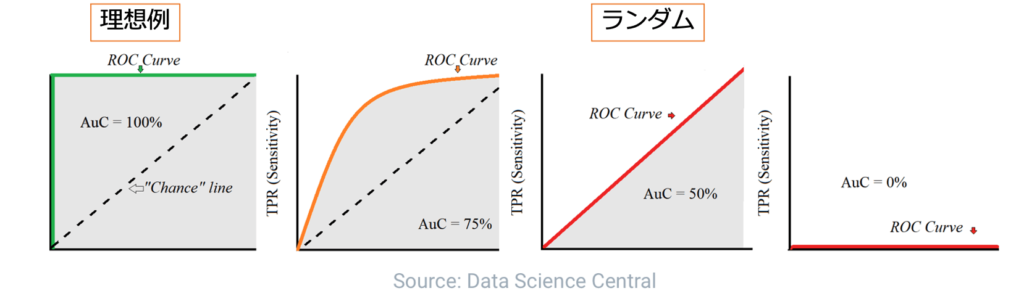
AUCはROC曲線(Receiver Operating Characteristic Curve)が描く曲線を元に算出されます。

 

ROC曲線は予測値を正とする閾値を1から0に動かしながら、その時の（偽陽性率、真陽性率）を(x, y)としてプロットすることで描かれます。

 

AUCはこのROC曲線の下の面積を指します。

 

理想的なROC曲線ではAUC1、ランダムのROC曲線はAUC0.5となります。

 

scikit learnのmetricsモジュールのroc_curve、aucを用いて求めることができます。

 

from sklearn import metrics
import matplotlib.pyplot as plt
import numpy as np

y_true = [0, 0, 0, 0, 1, 1, 1, 1]
y_pred = [0.2, 0.3, 0.6, 0.8, 0.4, 0.5, 0.7, 0.9]

# FPR, TPR, thresholds(しきい値) を算出
fpr, tpr, thresholds = metrics.roc_curve(y_true, y_pred)

# AUC
auc = metrics.auc(fpr, tpr)

# ROC曲線をプロット
plt.plot(fpr, tpr, label='ROC curve (area = %.2f)'%auc)
plt.legend()
plt.title('ROC curve')
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.grid(True)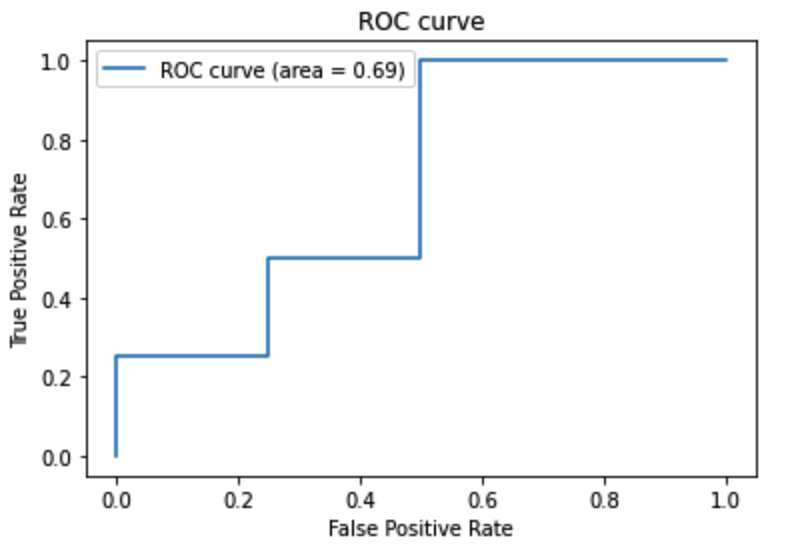

 

参考

・Kaggleで勝つデータ分析の技術

 

・予測した確率の評価再び。今更ですがLog損失（Log loss）を振り返る

 

さいごに

 

 

機械学習はプログラミング言語のPythonを用いれば、今持っている自分のパソコンですぐに実践することができます。

 

英語論文になっている手法もしっかりと勉強すれば、自分のパソコンで出来ます。

 

このサイトでは、プログラミングに興味のある医学生、医師のための情報を発信しております。

 

プログラミングの学習方法には大きく分けて、「独学」と「プログラミングスクール」の２つがあります。

 

当サイトでは一貫してプログラミングスクールを利用することをおすすめしています。

 

なぜなら、独学で勉強した私が非常に苦労したからです。

 

また私はプログラミングを学習するにあたり、師匠・メンターのような存在がいました。

 

わからないところは教えてもらっていました。

 

そのような環境でなければ０から独学で勉強するのはとても効率が悪いと思います。

 

詳しくは、プログラミングの独学は難しいです【私の失敗談】で紹介しています。

 

この記事が一人でも多くのプログラミングに興味のある方のお役に立てば幸いです。